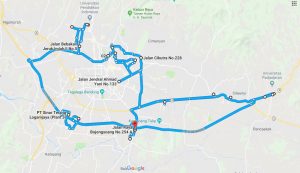
Bagaimana menentukan jalur optimum yang menghubungkan beberapa titik yang harus dikunjungi oleh seorang tenaga penjual (salesman)? William Rowan Hamilton, matematikawan asal dari Skotlandia memberikan solusi berupa lingkaran Hamiltonian yang menghubungkan seluruh titik dalam suatu graph dengan jarak atau biaya yang minimum.
Bagaimana mencari solusi untuk salesman atau distributor yang harus mengunjungi beberapa titik dalam suatu kota? Pada contoh ini kita akan buat solusi jalur perjalanan dari distributor gerai minuman di Kota Bandung.
Menentukan titik gerai
Titik lokasi gerai ditentukan dengan menetapkan titik dengan bantuan google maps. Pada kasus ini terdapat 20 titik gerai termasuk 1 tempat produksi.
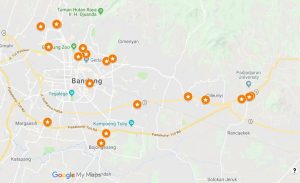
Menentukan jarak/biaya antar titik
Jarak antar titik dapat dicari dengan meminta google maps untuk membuatkan jalur dari dua titik. Apabila diasumsikan bahwa jalur dari titik A ke B berbeda dengan jalur dari titik B ke A, maka akan dilakukan sebanyak 380 permintaan. Dengan cara seperti ini, kita memerlukan kesabaran seperti Sisipus. Cara lain adalah dengan melakukan permintaan sekaligus dengan mengakses API Google.
mjarak1 <- google_distance(gc[1:5,]$latlon,gc$latlon,mode="driving",key="")
Ternyata dengan cara ini pun, kita tidak dapat melakukan permintaan sekaligus. Ada batasan waktu permintaan sehingga kita harus memecah permintaan menjadi beberapa bagian. Pada kasus 20 titik ini, yang tersimpan di dalam sebuah data frame bernama gc dilakukan permintaan per 5 titik, sehingga perlu 4 kali request. Cukup cepat dibandingkan harus 380 kali. Key harus diisi dengan key google api yang kita dapatkan saat mendaftar. Proses permintaan ini tidak gratis, tapi dalam batasan permintaan tertentu per hari, saat tulisan ini dibuat, masih gratis. Kita harus memasukan nomor kartu kredit/debit yang diterima oleh google sebagai pembayaran. Kalau kebetulan permintaan kita melampaui batas gratis harian, maka pihak google akan menarik sejumlah uang.
Mencari jalur optimum
Pencarian jalur lingkaran Hamiltonian yang menghubungkan seluruh titik menggunakan bantuan package "TSP" yang tersedia di CRAN-TSP.
Ah iya, sebelum bisa diproses dengan memanfaatkan fungsi yang tersedia di dalam package TSP, data yang dikirimkan oleh google harus kita bersihkan dulu, pilih sesuai dengan informasi yang kita inginkan.
Google memberikan dua pilihan, jarak antar dua titik diberikan dalam satuan waktu tempuh (detik) dan satuan jarak (km). Satuan waktu tempuh akan bergantung pada saat kita melakukan permintaan data, apakah ada kemacetan pada ruas jalan yang menghubungkan dua titik. Kode berikut dimaksudkan untuk mengambil bagian jarak (distance) dari data yang dikirim pada proses request data sebelumnya.
dist_mjarak1 <- t(sapply(mjarak1$rows$elements,unlist)[paste0("distance.value",c(1:20)),])
dur_mjarak1 <- t(sapply(mjarak1$rows$elements,unlist)[paste0("duration.value",c(1:20)),])
Baris kedua, adalah kode untuk mengambil data durasi. Selanjutnya kita ubah data yang bertipe string itu sebagai numerik.
dist_mjarak1 <- data.table(dist_mjarak1)[,lapply(.SD,as.numeric),]
dur_mjarak1 <- data.table(dur_mjarak1)[,lapply(.SD,as.numeric),]
Sebagaimana dijelaskan sebelumnya bahwa dari keduapuluh titik yang akan dihitung ini dilakukan permintaan sebanyak empat kali, sehingga selanjutnya harus digabungkan.
dist_mjarak <- as.matrix(rbind(dist_mjarak1,dist_mjarak2,dist_mjarak3,dist_mjarak4))
dur_mjarak <- as.matrix(rbind(dur_mjarak1,dur_mjarak2,dur_mjarak3,dur_mjarak4))
colnames(dist_mjarak) <- letters[1:20]
colnames(dur_mjarak) <- letters[1:20]
rownames(dist_mjarak) <- letters[1:20]
rownames(dur_mjarak) <- letters[1:20]
Kode tersebut menghasilkan dua matriks yang sudah siap untuk dilakukan pencarian solusi dengan menggunakan package TSP. horeee
Pencarian solusi jarak yang dihasilkan adalah sebagai berikut.
solusijarak <- solve_TSP(reformulate_ATSP_as_TSP(ATSP(dist_mjarak)),"nearest_insertion",start=40)
as.matrix(geraicokelat$Nama[lookup[unique(substr(labels(solusijarak),1,1))]])
Kita akan dapatkan urutan kunjungan dari setiap titik dengan titik awal yaitu titik produksi. Tentukan saja.
Plot titik-titik urutan dengan ke peta google lagi untuk mendapatkan sajian visual jalur yang diperoleh. Dengan cara biasa kita bisa mendapatkan jalur yang menghubungkan 10 titik. Ada trik tersendiri untuk membuat jalur dengan lebih dari 10 titik.